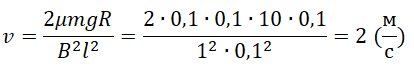Закон электромагнитной индукции • СПАДИЛО

Магнитный поток наглядно истолковывается как число линий магнитной индукции, пронизывающих поверхность площадью S. Поэтому скорость изменения этого числа есть не что иное, как скорость изменения магнитного потока.

Если за малое время ∆t магнитный поток поменялся на ∆Ф, то скорость изменения магнитного потока равна $\frac{Δ Φ}{Δ t}$ . Поэтому утверждение, которое вытекает непосредственно из опыта, можно сформулировать так:

Сила индукционного тока пропорциональная скорости изменения магнитного потока через поверхность, ограниченную контуром:

$I_{i} ~ \frac{Δ Φ}{Δ t}$

Известно, что в цепи появляется электрический ток в том случае, когда на свободные заряды проводника действуют сторонние силы. Работу этих сил при перемещении единичного положительного заряда вдоль замкнутого контура называют электродвижущей силой. Следовательно, при изменении магнитного потока через поверхность, ограниченную контуров, появляются сторонние силы, действие которых характеризуется ЭДС, называемой ЭДС индукции. Обозначают ее как $ε_{i}$ .

Согласно закону Ома для замкнутой цепи:

$I_{i} = \frac{ε_{i}}{R}$

Сопротивление проводника не зависит от изменения магнитного потока. Следовательно, сила индукционного тока пропорциональна скорости изменения магнитного потока только потому, что ЭДС индукции тоже пропорциональна этой скорости изменения потока.

Закон электромагнитной индукции

ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром.

$ε_{i} = ∣ ∣ ∣ \frac{Δ Φ}{Δ t} ∣ ∣ ∣$

Закон электромагнитной индукции формулируется именно для ЭДС, а не для силы тока. При такой формулировке закон выражает сущность явления, не зависящую от свойств проводников, в которых возникает индукционный ток.

Определение знака ЭДС индукции

На рисунке изображен замкнутый контур. Будем считать положительным направление обхода контура против часовой стрелки. Нормаль $\to n$ к контуру образует правый винт с направлением обхода.

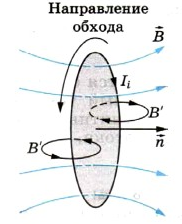
Пусть магнитная индукция $\to B$ внешнего магнитного поля направлена вдоль нормали к контуру и возрастает со временем. Тогда $Φ > 0$ и $\frac{Δ Φ}{Δ t} > 0$ . Согласно правилу Ленца индукционный ток создает магнитный поток $Φ^{‘} < 0$ . Линии магнитной индукции B’ магнитного поля индукционного тока изображены черным цветом. Следовательно, индукционный ток I_i согласно правилу буравчика направлен по часовой стрелке (против направления положительного обхода) и ЭДС индукции отрицательна. Поэтому в законе электромагнитной индукции должен стоять знак «–», указывающий на то, что $ε_{i} и \frac{Δ Φ}{Δ t}$ имеют разные знаки:

$ε_{i} = - \frac{Δ Φ}{Δ t}$

Пример №1. Магнитный поток через контур проводника сопротивлением 3∙10^–2 Ом за 2 с изменился на 1,2∙10^–2 Вб. Найдите силу тока в проводнике, если изменение потока происходило равномерно.

Известно, что:

$I_{i} = \frac{ε_{i}}{R}$

$ε_{i} = ∣ ∣ ∣ \frac{Δ Φ}{Δ t} ∣ ∣ ∣$

Следовательно:

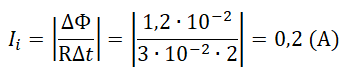
ЭДС индукции в движущихся проводниках

Электроны в неподвижном проводнике приводятся в движение электрическим полем, и это поле порождается переменным магнитным полем. Следовательно, изменяясь во времени, магнитное поле порождает электрическое поле. Но если проводник движется в постоянном во времени магнитном поле, то ЭДС индукции в проводнике обусловлена не вихревым электрическим полем, которое в этом случае не может возникнуть, а другой причиной.

При движении проводника его свободные заряды движутся вместе с ним. Поэтому на заряды со стороны магнитного поля действует сила Лоренца. Она и вызывает перемещение зарядов внутри проводника. ЭДС индукции, следовательно, имеет магнитное происхождение.

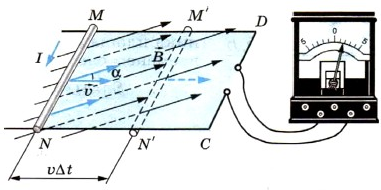
Вычислим ЭДС индукции, возникающую в проводнике, движущемся в однородном магнитном поле (см. рисунок). Пусть сторона контура MN длиной l скользит с постоянной скоростью $\to v$ вдоль сторон NC и MD, оставаясь все это время параллельной стороне CD. Вектор магнитной индукции $\to B$ однородного поля перпендикулярен проводнику и составляет угол $α$ с направлением его скорости.

Сила, с которой магнитное поле действует на движущуюся заряженную частицу, равна по модулю:

$F_{L} = | q | v B sin . α$

Направлена эта сила вдоль проводника MN. Работа силы Лоренца на пути l положительна и составляет:

$A = F_{L} l = | q | v B l sin . α$

Внимание!

Формула выше определяет неполную работу силы Лоренца. Кроме силы Лоренца имеется составляющая силы Лоренца, направленная против скорости проводника $\to v$ . Такая составляющая тормозит проводник и совершает отрицательную работу. В результате полная работа силы Лоренца оказывается равной нулю.

Электродвижущая сила индукции в проводнике MN равна по определению отношению работы по перемещению заряда q к этому заряду:

$ε_{i} = \frac{A}{| q |} = v B l sin . α$

Эта формула справедлива для любого проводника длиной l, движущегося со скоростью $\to v$ в однородном магнитном поле.

В других проводниках контура ЭДС равна нулю, так как проводники неподвижны. Следовательно, ЭДС во всем контуре MNCD равна $ε_{i}$ и остается неизменной, если скорость движения $\to v$ постоянна. Электрический ток при этом будет увеличиваться, так как при смещении проводника MN вправо уменьшается общее сопротивление контура.

С другой стороны, ЭДС индукции можно вычислить с помощью закона электромагнитной индукции. Магнитный поток через контур MNCD равен:

$Φ = B S cos . (90 ° - α) = B S sin . α$

угол $90 ° - α$ представляет собой угол между векторами $\to B$ и нормалью $\to n$ к поверхности контура, а S — площадь контура MNCD. Если считать, что в начальный момент времени t=0 проводник MN находится на расстоянии NC от проводника CD, то при перемещении проводника площадь S изменяется со временем следующим образом:

$S = l (N C - v t)$

За время ∆t площадь контура меняется на $Δ S = - l v Δ t$ . Знак «минус» указывает на то, что она уменьшается. Изменение магнитного потока за это время равно:

$Δ Φ = - B v l Δ t sin . α$

Следовательно:

$ε_{i} = - \frac{Δ Φ}{Δ t} = B v l sin . α$

Если весь контур MNCD движется в однородном магнитном поле, сохраняя свою ориентацию по отношению к вектору $\to B$ , то ЭДС индукции в контуре будет равна нулю, так как поток $Φ$ через поверхность, ограниченную контуром, не меняется. Объяснить это можно так. При движении контура в проводниках MN и CD возникают силы, действующие на электроны в направлениях от N к M и от C к D. Суммарная работа этих сил при обходе контура по часовой стрелке или против нее равна нулю.

Пример №2. Проводник длиной 50 см движется в однородном магнитном поле со скоростью 4 м/с перпендикулярно силовым линиям. Найдите разность потенциалов, возникающую на концах проводника, если вектор магнитной индукции 8 мТл.

50 см = 0,5 м

8 мТл = 8∙10^–3 Тл

Так как проводник движется перпендикулярно силовым линиям, то угол α равен 90 градусам, а синус прямого угла равен единице. Поэтому:

$ε_{i} = B v l sin . α = 8 \cdot 10^{- 3} \cdot 4 \cdot 0, 5 \cdot 1 = 16 \cdot 10^{- 3} (В)$

Задание EF17754

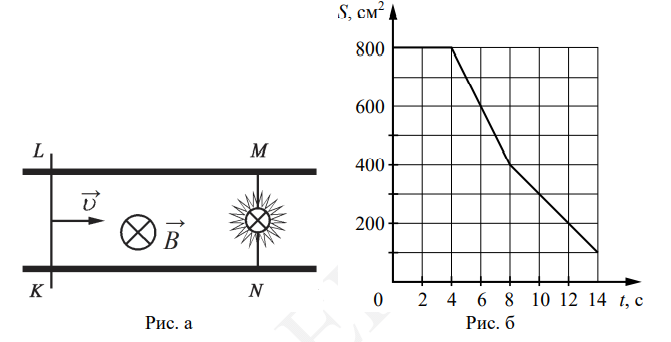
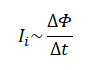
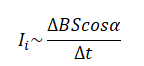
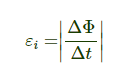
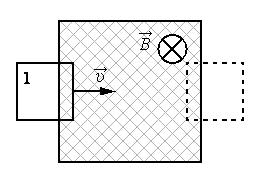В заштрихованной области на рисунке действует однородное магнитное поле, направленное перпендикулярно плоскости рисунка, В = 0,1 Тл. Проволочную квадратную рамку сопротивлением R=10Ом и стороной l=10см перемещают в плоскости рисунка поступательно со скоростью υ=1м/с. Чему равен индукционный ток в рамке в состоянии 1?

Ответ:

а) 1 мА

б) 5 мА

в) 10 мА

г) 20 мА

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Записать формулу для определения величины индукционного тока.

3.Записать закон электромагнитной индукции для движущихся проводников.

4.Выполнить решение в общем виде.

5.Подставить известные данные и вычислить искомую величину.

Решения

Запишем исходные данные:

• Модуль вектора магнитной индукции однородного магнитного поля: B = 0,1 Тл.

• Сопротивление внутри квадратной проволочной рамки: R = 10 Ом.

• Сторона рамки: l = 10 см.

• Скорость перемещения рамки: v = 1 м/с.

10 см = 0,1 м

Индукционный ток, возникающий в рамке, определяется по формуле:

$I_{i} = \frac{ε_{i}}{R}$

Закон электромагнитной индукции для движущихся проводников:

$ε_{i} = v B l sin . α$

Отсюда индукционный ток равен:

$I_{i} = \frac{v B l sin . α}{R}$

На рисунке вектор магнитной индукции направлен в сторону от наблюдателя. Следовательно, угол между направлением движения рамки и вектором магнитной индукции равен 90 градусам. А синус прямого угла равен единице. Тогда:

$I_{i} = \frac{v B l sin . 90 °}{R} = \frac{1 \cdot 0, 1 \cdot 0, 1 \cdot 1}{10} = 0, 001 (А) = 1 (м А)$

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17970

При вращении в однородном магнитном поле плоскости металлического кольца из тонкой проволоки вокруг оси, перпендикулярной линиям поля, максимальная сила индукционного тока, возникающего в кольце, равна I₁. Чему будет равна максимальная сила индукционного тока I₂ в этом кольце при уменьшении скорости вращения кольца в 2 раза?

Ответ:

а) I₂ = 2I₁

б) I₂ = I₁

в) I₂ = 0,5I₁

г) I₂ = 4I₁

Алгоритм решения

1.Записать закон электромагнитной индукции.

2.Установить зависимость между величиной индукционного тока и скоростью вращения рамки.

3.Определить, как изменится величина индукционного тока в кольце при уменьшении скорости ее вращения.

Решение

Запишем формулу закона электромагнитной индукции:

$ε_{i} = ∣ ∣ ∣ \frac{Δ Φ}{Δ t} ∣ ∣ ∣$

Известно, что отношение изменения магнитного потока ко времени его изменения — это величина, характеризующая скорость этого изменения. Если кольцо в однородном магнитном поле вращать медленнее, то и магнитный поток начнет менять медленнее. Так как ЭДС индукции прямо пропорционально зависит от скорости изменения магнитного потока, то при уменьшении скорости вращения кольца в 2 раза она также уменьшится вдвое.

Также известно, что индукционный ток в рамке определяется формулой:

$I_{i} = \frac{ε_{i}}{R}$

Видно, что индукционный ток и ЭДС индукции — прямо пропорциональные величины. Следовательно, при уменьшении ЭДС индукции вдвое сила индукционного тока тоже уменьшится в 2 раза. Отсюда следует, что I₂ = 0,5I₁.

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18860

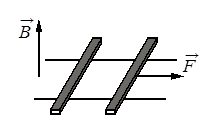По горизонтально расположенным шероховатым рельсам с пренебрежимо малым сопротивлением могут скользить два одинаковых стержня массой m = 100 г и сопротивлением R = 0,1 Ом каждый. Расстояние между рельсами l = 10 см, а коэффициент трения между стержнями и рельсами μ = 0,1 Рельсы со стержнями находятся в однородном вертикальном магнитном поле с индукцией B = 1 Тл (см. рисунок). Под действием горизонтальной силы, действующей на первый стержень вдоль рельс, оба стержня движутся поступательно равномерно с разными скоростями. Какова скорость движения первого стержня относительно второго? Самоиндукцией контура пренебречь. Ответ записать в системе СИ.

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения в СИ.

2.Записать закон электромагнитной индукции для двигающихся стержней.

3.Выполнить решение задачи в общем виде.

4.Подставить неизвестные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса стержней:

m_{1} = m_{2} = m = 100

г.

• Сопротивление стержней:

R_{1} = R_{2} = R = 0, 1

Ом.

• Расстояние между рельсами: l = 10 см.

• Коэффициент трения между стержнями и рельсами: μ = 0,1.

• Модуль вектора магнитной индукции магнитного поля: B = 1 Тл.

• Угол между вектором магнитной индукцией и вектором скорости стержней: α = 90 градусов (синус прямого угла равен «1»).

100 г = 0,1 кг

10 см = 0,1 м

Когда под действием некой силы начинается двигаться первый стержень, магнитный поток, пронизывающий контур, образованные проводящими рельсами и двумя стержнями, меняется. Это приводит к возникновению в этом контуре электродвижущей силы, которую можно определить с помощью закона электромагнитной индукции для двигающихся стержней:

$ε_{i} = v B l sin . α$

Причем v — это разность скоростей стержней (v₂ – v₁), которая характеризует скорость изменения площади проводящего контура.

Индукционный ток, возникающей в этом контуре, можно выразить, используя закон Ома:

$ε_{i} = I R_{к}$

где $R_{к}$ — сопротивление контура. Так как стержни соединяются последовательно, и их сопротивления равны R, а сопротивление рельсов ничтожно мало, сопротивление контура равно:

$R_{к} = 2 R$

Отсюда закон Ома принимает вид:

$ε_{i} = 2 I R$

Тогда ток в контуре равен:

$I = \frac{ε_{i}}{2 R} = \frac{v B l sin . α}{2 R}$

С одной стороны на стержни действует сила Ампера, с другой — сила трения, возникающего между ними и рельсами. Так как стержни движутся равномерно, равнодействующая сил, приложенных к ним, равна нулю. Следовательно, сила трения и сила Ампера компенсируют друг друга (их модули равны):

$F_{т р} = F_{А}$

$μ m g = B I l sin . α$

Подставим сюда выражение, полученное для силы тока в контуре:

$μ m g = B \frac{v B l sin . α}{2 R} l sin . α = \frac{{v B}^{2} l^{2} {sin}^{2} . α}{2 R}$

Отсюда скорость равна:

$v = \frac{2 μ m g R}{B^{2} l^{2} {sin}^{2} . α}$

Так как синус угла равен «1»:

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 5.6k