Архимедова сила | теория по физике 🧲 гидростатика

Определение

Архимедова сила (выталкивающая сила, подъемная сила) — сила, с которой жидкость или газ выталкивают погруженное в них тело.

Полезно знать и понимать!

Причина возникновения выталкивающей силы: нижняя грань тела находится на большей глубине, чем верхняя, поэтому давление жидкости снизу больше, чем сверху. Из-за разницы в давлениях возникает выталкивающая сила.
Архимедова сила всегда направлена вертикально вверх.
Архимедова сила равна разности сил давления на нижнюю и верхнюю грани:

F_A = F_H – F_B

Также выталкивающая сила равна разности веса тела в воздухе и веса тела в жидкости:

F_A = P_возд – P_ж

Модуль выталкивающей силы определяется с помощью закона Архимеда.

Закон Архимеда

Выталкивающая сила равна весу вытесненной жидкости.

F_A = P_ж

Частные случаи определения архимедовой силы

Полное погружение
	Архимедова сила равна произведению плотности жидкости, объема тела и ускорения свободного падения: F_A = ρ_жV_тg V_т — объем погруженного в жидкость тела.
Неполное погружение
	Архимедова сила равна произведению плотности жидкости, объема погруженной части тела и ускорения свободного падения: F_A = ρ_жV_п.ч.g V_п.ч. — объем погруженной в жидкость части тела.

Внимание! Если тело погружено в газ, то в формуле нужно использовать плотность этого газа.

Пример №1. При взвешивании груза в воздухе показание динамометра равно 1 Н. При опускании груза в воду показание динамометра уменьшается до 0,6 Н. Найдите значение выталкивающей силы.

Выталкивающая сила равна разности веса тела в воздухе и веса тело в воде. Следовательно:

F_A = P_возд – P_ж = 1 – 0,6 = 0,4 (Н)

Воздухоплавание

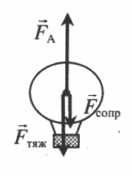
Подъемной силой воздушного шара служит архимедова сила, равная:

F_A = ρ_воздV_шg

Подъемной силе противостоят сила тяжести и сила сопротивления воздуха:

F_тяж = (M_шара + m_газа + m_корз + m_груза)g

F_сопр

Управление шаром:

чтобы взлететь, шар заполняют нагретым воздухом или газом, плотность которого меньше плотности окружающего воздуха;
чтобы увеличить высоту полета, с шара сбрасывают балласт;
чтобы спуститься на землю, газ охлаждают.

Пример №2. Аэростат объемом 1000 м³ заполнен гелием. Плотность гелия 0,18 кг/м³, плотность воздуха 1,29 кг/м³. Какая выталкивающая сила действует на аэростат?

Выталкивающая сила зависит только от плотности окружающей среды и объема погруженного в него тела. Так как аэростат погружен в воздух полностью:

F_A = ρ_вV_тg = 1,29∙1000∙10 = 12,9 (кН)

Архимедова сила и законы Ньютона

Если тело полностью погружено в жидкость (или газ):

Архимедова сила равна: F_A = ρ_жV_тg.
Сила тяжести, действующая на тело: F_тяж = mg = ρ_тV_тg.

Частный случай

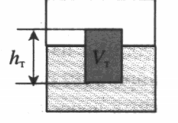
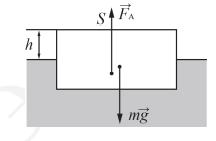
Определить минимальную массу груза, который следует положить на плоскую однородную льдину площадью S, чтобы она полностью погрузилась в воду. Толщина льдины h, а плотность льда ρ_л, плотность воды ρ_в.

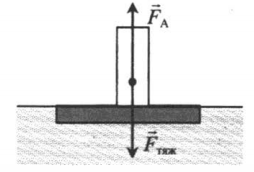
Второй закон Ньютона в векторной форме для льдины, полностью погруженной в воду (она не тонет и не всплывает):

${\to F}_{A} + {\to F}_{т я ж} = 0$

Так как эти силы направлены в противоположные стороны:

F_A = F_тяж

Архимедова сила, действующая только на льдину, равна:

F_A = ρ_вV_лg

Сила тяжести равна сумме масс льдины и груза:

F_тяж = (m_л + m_гр)g

Массу льдины можно выразить через произведение ее плотности на объем, равные произведению ее площади на толщину:

m_л = ρ_лSh

Пример №3. Какую силу надо приложить, чтобы поднять под водой камень, масса которого 30 кг, а объем 12 000 см³?

12 000 куб. см = 0,012 куб. м

Чтобы поднять под водой камень, потребуется сила, равная разности силе тяжести и архимедовой силы, действующей на этот камень:

F = F_тяж – F_A = mg – ρ_вV_тg = 30∙10 – 1000∙0,012∙10 = 180 (Н)

Условия плавания тел

На любое тело, погруженное в жидкость или газ, действуют две противоположно направленные силы: сила тяжести и архимедова сила. Направление движения тела зависит от того, какая из этих сил больше по модулю:

Тело тонет, если: mg > F_A; ρ_т > ρ_ж.
Тело плавает в толще среды, если: mg = F_A; ρ_т = ρ_ж.
Тело всплывает, если: mg < F_A; ρ_т < ρ_ж.

Внимание! Тело, имеющее плотность меньшую, чем плотность жидкости, в которой оно плавает, будет находиться на поверхности, погрузившись в жидкость частично.

Если тело плавает на поверхности:

Архимедова сила и сила тяжести, действующие на него, равны: F_A= F_тяж.
Сила тяжести равна: F_тяж = mg = ρ_тV_тg.
Архимедова сила равна: F_A = ρ_жV_п.ч.g.
Взаимосвязь между объемом и высотой тела правильной формы: V = Sh.

Варианты условий задач на условия плавания тел

Сплошное тело объемом V_т плавает в воде. Причем под водой находится 3/4 его объема. Определите силу тяжести, действующую на тело. Плотность воды ρ_в.

Второй закон Ньютона в векторной форме:

${\to F}_{A} + {\to F}_{т я ж} = 0$

Отсюда (проекция на вертикальную ось):

F_A = F_тяж

F_тяж = 3ρ_вV_тg/4

Какая часть (в процентах) айсберга находится под водой? Плотность льда ρ_л, а воды ρ_в.

Второй закон Ньютона в векторной форме:

${\to F}_{A} + {\to F}_{т я ж} = 0$

Отсюда (проекция на вертикальную ось):

F_A = F_тяж

Отсюда:

ρ_лV_лg = ρ_вV_п.ч.g

Ускорение свободного падения взаимоуничтожается. Чтобы найти погруженную часть айсберга в процентах, нужно:

$\frac{V_{п . ч .}}{V_{л}} = \frac{ρ_{л}}{ρ_{в}}$

Найденное отношение остается умножить на 100%.

Полое тело плотностью ρ_т плавает в воде, погрузившись на 1/5 своего объема. Найдите объем полости V_п, если объем тела V_т, а плотность воды ρ_в.

Второй закон Ньютона в векторной форме:

${\to F}_{A} + {\to F}_{т я ж} = 0$

Отсюда (проекция на вертикальную ось):

F_A = F_тяж

Отсюда:

ρ_вV_п.ч.g = ρ_т(V_т – V_п)g

Преобразовав выражение, получим:

$V_{п} = \frac{V_{т} (5 ρ_{т} - ρ_{в})}{5 ρ_{т}}$

Пример №4. Кубик массой 40 г и объемом 250 см³ плавает на поверхности воды. Найдите значение выталкивающей силы, действующей на кубик.

40 г = 0,04 кг

250 см³ = 250∙10^–6 м³

Так как тело плавает, Архимедова сила будет равна по модулю силе тяжести, которая определяется формулой:

F_A = F_тяж = 0,04∙10 = 0,4 (Н)

Текст: Алиса Никитина, 12.2k 👀

Задание ЕГЭ-Ф-ДВ2023-25

Плоская льдина плавает в воде, выступая над её поверхностью на h = 0,04 м. Определите массу льдины, если площадь её поверхности S = 2500 см². Плотность льда равна 900 кг/м³. .

Алгоритм решения:

1.Записать исходные данные.

2.Перевести единицы измерения величин в СИ.

3.Сделать рисунок. Установить, какие силы действуют на плоскую льдину. Обозначить их на рисунке.

4.Составить уравнение проекций сил.

5.Сделать необходимые преобразования и выразить искомую величину.

6.Подставить известные данные и произвести вычисления.

Решение:

Запишем исходные данные:

• Высота части льдины, выступающей над поверхностью воды: h = 0,04 м.

• Площадь поверхности льдины: S = 2500 см².

• Плотность льдины: ρ = 900 кг/м³.

В СИ нужно перевести только площадь:

S = 2500 см²= 2500/10 000 м³ = 0,25 м³

Сделаем рисунок и обозначим на нем силы, которые действуют на льдину:

Льдина плавает на поверхности воды, некоторая ее часть выступает над ней. Она не тонет и не всплывает. Следовательно, все приложенные к ней силы уравновешены. В частности, на нее действуют 2 силы:

• Сила Архимеда, направленная вверх.

• Сила тяжести, направленная вниз.

Так как силы уравновешены и направлены вдоль одной прямой, их проекции равны:

Или:

m — масса льдины, $ρ_{ж}$ — плотность жидкости, в которую погружена льдина (то есть, воды). V_т — объем той части льдины, которая погружена в воду. Его можно вычислить по формуле:

За H мы обозначили полную высоту льдины.

Следовательно:

Мы также можем считать, что масса льдины равна:

V — полный объем льдины, ρ — ее плотность.

Приравняем правые части уравнений:

Или:

Найдем высоту льдины:

Отсюда масса льдины равна:

Подставим известные данные и вычислим массу льдины:

Ответ: 90

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18524

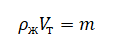
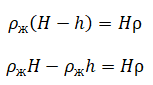
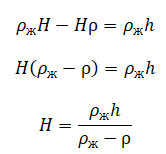
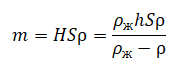
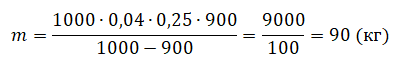
Деревянный шарик плавает в стакане с водой. Как изменятся сила тяжести и архимедова сила, действующие на шарик, если он будет плавать в подсолнечном масле?

Для каждой величины определите соответствующий характер изменения:

Увеличится.
Уменьшиться.
Не изменится.

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Записать условие плавания тел.
На основании условия плавания тел сделать вывод о том, как изменятся указанные физические величины.

Решение

По условию задачи деревянный шарик плавает на поверхности воды. Но это возможно, лишь когда архимедова сила равна силе тяжести:

F_A_в = F_тяж

Если шарик будет плавать в подсолнечном масле, также можно применить условие плавания тел:

F_A_м = F_тяж

Сила тяжести зависит только от массы тела, которая остается неизменной. Поэтому сила тяжести тоже не меняется. Но из этого следует:

F_A_в = F_A_м

Это возможно благодаря тому, что объем погруженной части шарика в масло будет больше объема погруженной части шарика в воду. Этим компенсируется разница в плотностях жидкостей, но архимедова сила при этом остается неизменной.

Верный ответ: 33.

Ответ: 33

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18477

Ученик изучает силу Архимеда, действующую на тела, полностью погружённые в жидкость. В его распоряжении имеется установка, состоящая из ёмкости с водой и сплошного деревянного шарика объёмом 30 см³. Какая из следующих установок необходима ещё ученику для того, чтобы на опыте обнаружить зависимость силы Архимеда от объёма тела?

$№$ установки	Жидкость, налитая в ёмкость	Объём шарика	Материал, из которого сделан шарик
1	вода	30 см³	сталь
2	вода	20 см³	дерево
3	керосин	20 см³	дерево
4	подсолнечное масло	30 см³	сталь

Ответ:

а) установка $№$ 1

б) установка $№$ 2

в) установка $№$ 3

г) установка $№$ 4

Алгоритм решения

Сделать анализ задачи. Определить, какие величины в опыте остаются постоянными.
Определить, какие величины должны быть в опыте переменными.

Решение

Ученик изучает силу Архимеда, действующую на тела, полностью погружённые в жидкость. В формулировке слово «жидкость» используется в единственном числе. Следовательно, жидкость во всех опытах будет одной и той же (плотность жидкости будет постоянной). У ученика уже есть установка, в которую входит емкость с водой. Поэтому во второй установке в качестве жидкости тоже должна использоваться вода. Варианты 3 и 4 исключаются.

В формулировки задачи также говорится о «телах». Они могут быть выполнены из разных материалов, и они могут иметь разный объем. Но известно, что архимедова сила зависит только от объема тела. Поэтому во второй установке нужно использовать тело другого объема. В вариантах 1 и 2 этому условию соответствует деревянный шарик объемом 20 куб. см (так как в первой установке используется шарик объемом 30 куб. см).

Отсюда верный ответ: б.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22696

Необходимо экспериментально изучить зависимость силы Архимеда, действующей на тело, погружённое в жидкость, от плотности жидкости.

Какие две установки следует использовать для проведения такого исследования?

Алгоритм решения

Установить цели опыта.
Сделать вывод о том, какие величины в опыте должны быть постоянными, а какие — переменными.
Выбрать установки, соответствующие выводу.

Решение

В опыте нужно изучить зависимость силы Архимеда, действующей на тело, погружённое в жидкость, от плотности жидкости. Это значит, что плотность жидкости — величина переменная. Все остальные величины при этом должны оставаться постоянным. Поэтому нам нужны установки с разными жидкостями, но одинаковыми телами. Этому условию соответствуют две установки: «а» и «д».

Ответ: ад

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18057

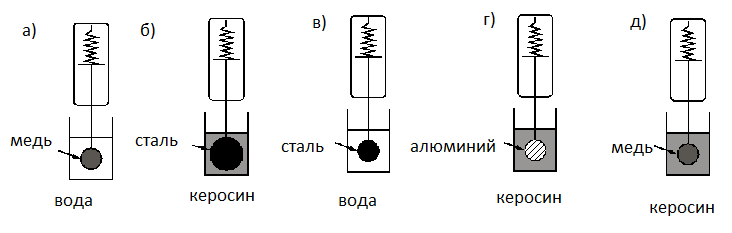
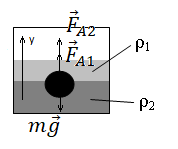
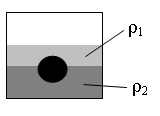На границе раздела двух несмешивающихся жидкостей, имеющих плотности ρ₁ = 400 кг/м³ и ρ₂ = 2ρ₁, плавает шарик (см. рисунок). Какой должна быть плотность шарика ρ, чтобы выше границы раздела жидкостей была одна четверть его объёма?

Алгоритм решения

1.Записать исходные данные.

2.Выполнить рисунок.

3.Записать второй закон Ньютона в векторной форме.

4.Записать второй закон Ньютона в проекции на ось ординат.

5.Выполнить общее решение.

6.Вычислить искомую величину, подставив известные данные.

Решение

Запишем исходные данные:

• Плотность первой жидкости: ρ₁ = 400 кг/м³.

• Плотность второй жидкости: ρ₂ = 2ρ₁.

• Объем шарика: V.

• Объем шарика выше границы раздела двух жидкостей: V₁ = V/4.

• Объем шарика выше границы раздела двух жидкостей: V₂ = 3V/4.

Построим рисунок и укажем все силы, действующие на шарик:

Запишем второй закон Ньютона в векторном виде:

$m \to g + {\to F}_{A 1} + {\to F}_{A 2} = 0$

Запишем второй закон Ньютона в виде проекции на ось ординат:

$m g = F_{A 1} + F_{A 2}$

Выразим массу тела через его объем и плотность, выразим выталкивающие силы через закон Архимеда и получим:

$ρ V g = ρ_{1} g V_{1} + ρ_{2} g V_{2}$

Преобразуем выражение, сократив ускорение свободного падения и подставив выражения для объемов погруженных в жидкости частей тела, а также выражение для плотности второй жидкости:

$ρ V = \frac{ρ_{1} V}{4} + \frac{2 ρ_{1} 3 V}{4}$

Объемы сокращаются. Остается:

$ρ = \frac{ρ_{1}}{4} + \frac{2 ρ_{1} 3}{4} = \frac{7 ρ_{1}}{4} = \frac{7 \cdot 400}{4} = 700 (\frac{к г}{м^{3}})$

.

Ответ: 700

pазбирался: Алиса Никитина | обсудить разбор

ЕГЭ по физике

Вся теория

• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

Закон Архимеда

Воздухоплавание

Архимедова сила и законы Ньютона

Условия плавания тел

Варианты условий задач на условия плавания тел

Задание ЕГЭ-Ф-ДВ2023-25

Задание EF18524

Задание EF18477

Задание EF22696

Задание EF18057

ЕГЭ по физике

Вся теория

Добавить комментарий Отменить ответ