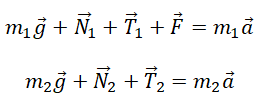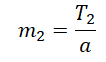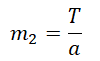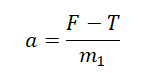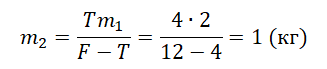Иногда в системе движется не одно, а два связанных между собой тела. Тогда описание движения с применением законов Ньютона включает в себя описания движения каждого из этих тел.
Движение тел по горизонтали без трения
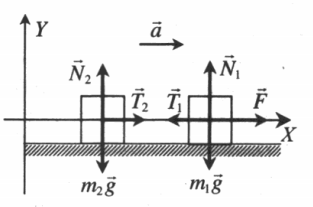
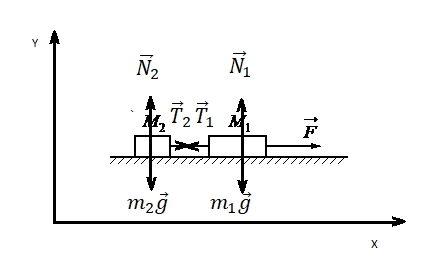
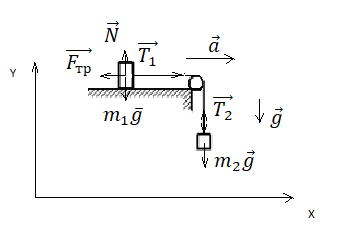
Движение по горизонтали с учетом сил трения
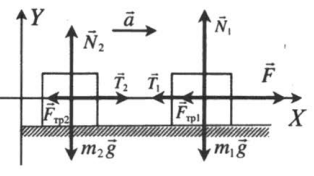
Вертикальное движение тел (m1 > m2)
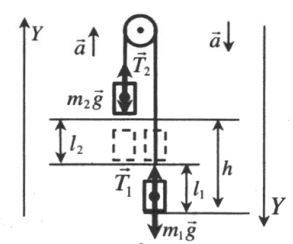
h — расстояние между телами. l1 и l2 — перемещение тела 1 и тела 2 соответственно. Перемещения обоих тел равны, поэтому: l1 = l2 = l.
На один из грузов положили довесок
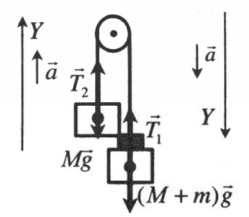
Пример №1. На нити, переброшенной через неподвижный блок, подвешены грузы массами m и 2m. С каким ускорением будут двигаться грузы, если их отпустить? Трением в блоке пренебречь.
Строим чертеж:
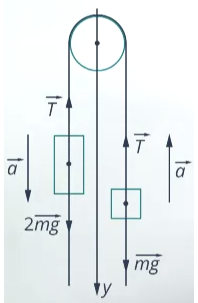
Записываем второй закон Ньютона для каждого из тел. Для первого тела он будет иметь вид:
Для второго тела II закон Ньютона примет следующий вид:
Запишем проекции на ось OУ для каждого из тел:
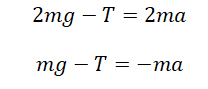
Выразим силы натяжения нити для каждого из тел и приравняем их правые части:
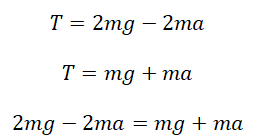
Сделаем несколько преобразований:
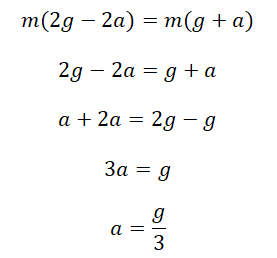
Это значит, если отпустить грузы, они будут двигаться с ускорением, втрое меньшим по сравнению с ускорением свободного падения. Приблизительно оно будет равно 3,33 м/с2.
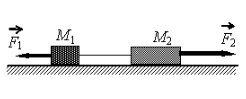 Два груза массами соответственно М1 = 1 кг и М2 = 2 кг, лежащие на гладкой горизонтальной поверхности, связаны невесомой и нерастяжимой нитью. На грузы действуют силы
Два груза массами соответственно М1 = 1 кг и М2 = 2 кг, лежащие на гладкой горизонтальной поверхности, связаны невесомой и нерастяжимой нитью. На грузы действуют силы 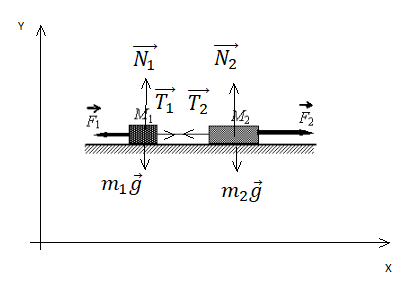
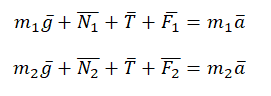
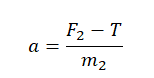
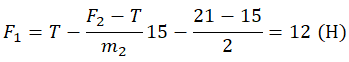
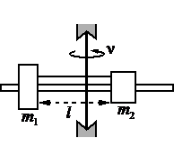 На вертикальной оси укреплена гладкая горизонтальная штанга, по которой могут перемещаться два груза массами m1 = 200 г и m2 = 300 г, связанные нерастяжимой невесомой нитью длиной l = 20 см. Нить закрепили на оси так, что грузы располагаются по разные стороны от оси и натяжение нити с обеих сторон от оси при вращении штанги одинаково (см. рисунок). Определите модуль силы натяжения Т нити, соединяющей грузы, при вращении штанги с частотой 600 об/мин.
На вертикальной оси укреплена гладкая горизонтальная штанга, по которой могут перемещаться два груза массами m1 = 200 г и m2 = 300 г, связанные нерастяжимой невесомой нитью длиной l = 20 см. Нить закрепили на оси так, что грузы располагаются по разные стороны от оси и натяжение нити с обеих сторон от оси при вращении штанги одинаково (см. рисунок). Определите модуль силы натяжения Т нити, соединяющей грузы, при вращении штанги с частотой 600 об/мин.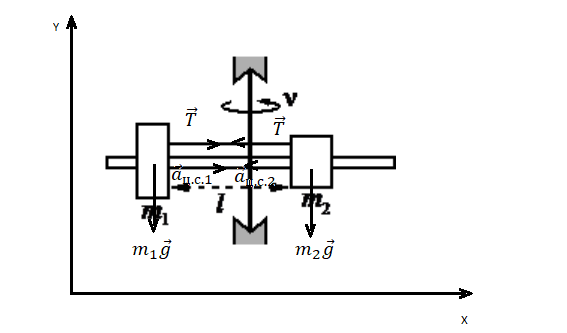
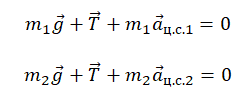
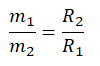
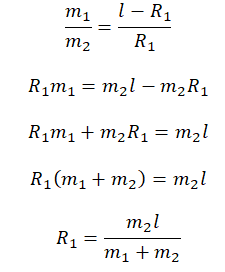
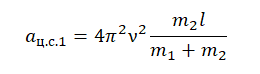
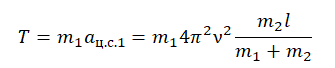
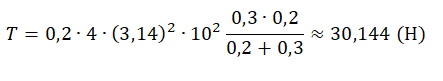
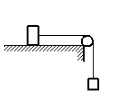 По горизонтальному столу из состояния покоя движется брусок массой 0,9 кг, соединённый с грузом массой 0,3 кг невесомой нерастяжимой нитью, перекинутой через гладкий невесомый блок (см. рисунок). Коэффициент трения бруска о поверхность стола равен 0,2. Натяжение вертикальной части нити равно:
По горизонтальному столу из состояния покоя движется брусок массой 0,9 кг, соединённый с грузом массой 0,3 кг невесомой нерастяжимой нитью, перекинутой через гладкий невесомый блок (см. рисунок). Коэффициент трения бруска о поверхность стола равен 0,2. Натяжение вертикальной части нити равно:
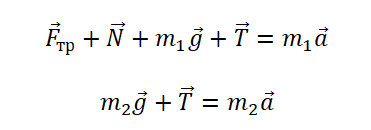
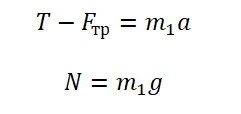
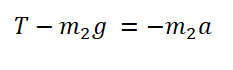

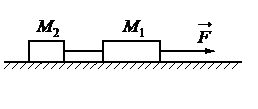 Два груза, связанные нерастяжимой и невесомой нитью, движутся по гладкой горизонтальной поверхности под действием постоянной горизонтальной силы F, приложенной к грузу М1 = 2 кг (см. рисунок). Нить обрывается при значении силы натяжения нити 4 Н, при этом модуль силы F равен 12 H. Чему равна масса второго груза М2?
Два груза, связанные нерастяжимой и невесомой нитью, движутся по гладкой горизонтальной поверхности под действием постоянной горизонтальной силы F, приложенной к грузу М1 = 2 кг (см. рисунок). Нить обрывается при значении силы натяжения нити 4 Н, при этом модуль силы F равен 12 H. Чему равна масса второго груза М2?