Любые заряженные тела создают вокруг себя электростатическое поле. Рассмотрим особенности электростатического поля, создаваемого точечным зарядом и заряженной сферой.
Электростатическое поле точечного заряда
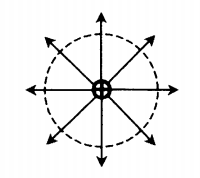
Направление силовых линий электростатического поля точечного заряда
| Положительный заряд +Q | Отрицательный заряд –Q |
 |
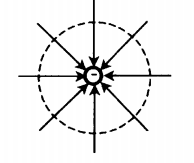 |
| У положительного заряда силовые линии направлены по радиальным линиям от заряда. | У отрицательного заряда силовые линии направлены по радиальным линиям к заряду. |
Модуль напряженности не зависит от значения пробного заряда q0:
E=FKq0=kQq0r2q0=kQr2
Модуль напряженности точечного заряда в вакууме:
E=kQr2
Модуль напряженности точечного заряда в среде:
E=kQεr2
Сила Кулона:
−FKулона=q−E
Потенциал не зависит от значения пробного заряда q0:
φ=Wpqo=±kQq0rq0=±kQr
Потенциал точечного заряда в вакууме:
φ=±kQr
Потенциал точечного заряда в среде:
φ=±kQεr
Внимание! Знак потенциала зависит только от знака заряда, создающего поле.
Эквипотенциальные поверхности для данного случая — концентрические сферы, центр которых совпадает с положением заряда.
Работа электрического поля по перемещению точечного заряда:
A12=±q(φ1−φ2)
Пример №1. Во сколько раз увеличится модуль напряженности электрического поля, созданного точечным зарядом Q в некоторой точке, при увеличении значения этого заряда в 5 раз?
Модуль напряженности электрического поля, созданного точечным зарядом, определяется формулой:
E=kQεr2
Формула показывает, что модуль напряженности и электрический заряд — прямо пропорциональные величины. Следовательно, если заряд, который создает поле, увеличится в 5 раз, то модуль напряженности создаваемого поля тоже увеличится в 5 раз.
Электростатическое поле заряженной сферы
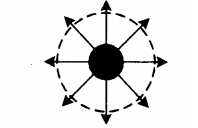
Направление силовых линий электростатического поля заряженной сферы:
| Положительно заряженная сфера +Q | Отрицательно заряженная сфера –Q |
 |
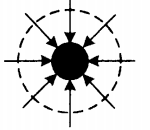 |
| У положительно заряженной сферы силовые линии — это радиальные линии, которые начинаются из этой сферы. | У отрицательно заряженной сферы силовые линии — это радиальные линии, которые заканчиваются в этой сфере. |
Модуль напряженности электростатического поля заряженной сферы:
| Внутри проводника (расстояние меньше радиуса сферы, или r < R) |
E=0 |
| На поверхности проводника (расстояние равно радиусу сферы, или r = R) |
E=kQR2 |
| Вне проводника (расстояние больше радиуса сферы, или r > R) |
E=kQr2=kQ(R+a)2 a — расстояние от поверхности сферы до изучаемой точки. r — расстояние от центра сферы до изучаемой точки. |
Сила Кулона:
−FK=q−E
Потенциал:
| Внутри проводника и на его поверхности (r < R или r = R) |
φ=±kQR |
| Вне проводника (r > R) |
φ=±kQr=±φ=±kQR+a |
Пример №2. Определить потенциал электростатического поля, создаваемого заряженной сферой радиусом 0,1 м, в точке, находящейся на расстоянии 0,2 м от этой сферы. Сфера заряжена положительна и имеет заряд, равный 6 нКл.
6 нКл = 6∙10–9 Кл
Так как сфера заряжена положительно, то потенциал тоже положителен:
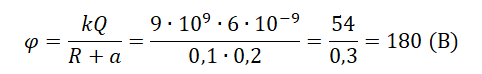
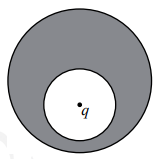 В нижней половине незаряженного металлического шара располагается крупная шарообразная полость, заполненная воздухом. Шар находится в воздухе вдали от других предметов. В центр полости
помещён положительный точечный заряд q > 0 (см. рисунок). Нарисуйте картину линий напряжённости электростатического поля внутри полости, внутри проводника и снаружи шара. Если поле отсутствует, напишите в данной области:
В нижней половине незаряженного металлического шара располагается крупная шарообразная полость, заполненная воздухом. Шар находится в воздухе вдали от других предметов. В центр полости
помещён положительный точечный заряд q > 0 (см. рисунок). Нарисуйте картину линий напряжённости электростатического поля внутри полости, внутри проводника и снаружи шара. Если поле отсутствует, напишите в данной области: 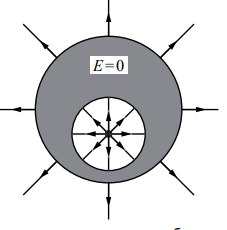
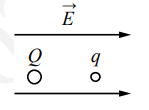 В однородном электрическом поле с напряжённостью E =18 В/м находятся два точечных заряда: Q = −1 нКл и q = +5 нКл с массами M = 5 г и m =10 г соответственно (см. рисунок). На каком расстоянии d друг от друга находятся заряды, если их ускорения совпадают по величине и направлению? Сделайте рисунок с указанием всех сил, действующих на заряды. Силой тяжести пренебречь.
В однородном электрическом поле с напряжённостью E =18 В/м находятся два точечных заряда: Q = −1 нКл и q = +5 нКл с массами M = 5 г и m =10 г соответственно (см. рисунок). На каком расстоянии d друг от друга находятся заряды, если их ускорения совпадают по величине и направлению? Сделайте рисунок с указанием всех сил, действующих на заряды. Силой тяжести пренебречь.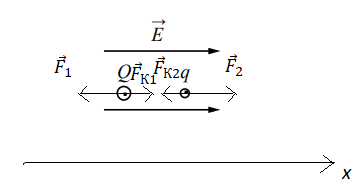
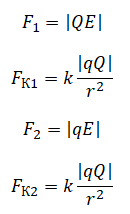
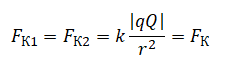
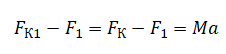
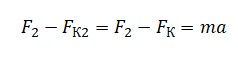
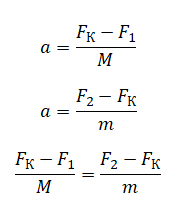
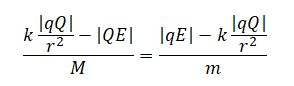
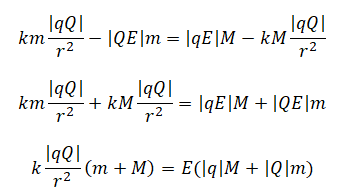
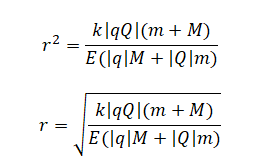
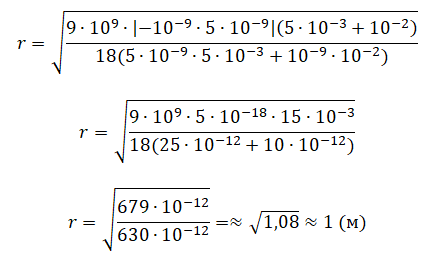
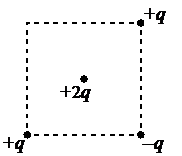 В трёх вершинах квадрата размещены точечные заряды: +q,
В трёх вершинах квадрата размещены точечные заряды: +q, 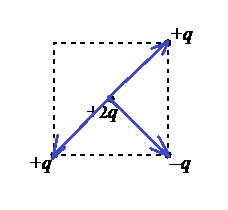
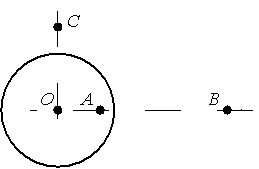 На неподвижном проводящем уединённом шарике радиусом R находится заряд Q. Точка O – центр шарика, OA = 3R/4, OB = 3R, OC = 3R/2. Модуль напряжённости электростатического поля заряда Q в точке C равен EC. Определите модуль напряжённости электростатического поля заряда Q в точке A и точке B?
На неподвижном проводящем уединённом шарике радиусом R находится заряд Q. Точка O – центр шарика, OA = 3R/4, OB = 3R, OC = 3R/2. Модуль напряжённости электростатического поля заряда Q в точке C равен EC. Определите модуль напряжённости электростатического поля заряда Q в точке A и точке B?