Совершение работы телом не проходит бесследно. Рассмотрим, например, часы с пружинным заводом. При заводе часов состояние системы (часового механизма) меняется так, что она приобретает способность совершать работу в течение длительного времени. Пружина поддерживает движение всех колес, стрелок и маятника, испытывающих сопротивление движению, вызванное трением. По мере хода часов способность пружины совершать работу постепенно утрачивается. Состояние пружины меняется.
Если тело или система тел могут совершить работу, говорят, что они обладает механической энергией.
Виды механической энергии
В механике состояние системы определяется положением тел и их скоростями. Поэтому в ней выделяют два вида энергии: потенциальную и кинетическую.
Пример №1. Мальчик подбросил футбольный мяч массой 0,4 кг на высоту 3 м. Определить его потенциальную и кинетическую энергию в верхней точке.
Потенциальная энергия мяча в поле тяготения Земли равна:
Ep = mgh = 0,4∙10∙3 = 12 (Дж)
В верхней точке полета скорость мяча равна нулю. Следовательно, кинетическая энергия мяча в этой точке тоже будет равна нулю:
Ek = 0 (Дж).
Теорема о кинетической энергии
Пример №2. Скорость движущегося автомобиля массой 1 т изменилась с 10 м/с до 20 м/с. Чему равна работа равнодействующей силы?
Сначала переведем единицы измерения в СИ: 1 т = 1000 кг. Работа равна изменения кинетической энергии, следовательно:
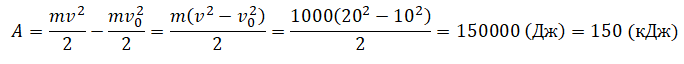
Работа и потенциальная энергия тела, поднятого над Землей
Величина потенциальной энергии зависит от выбора нулевого уровня энергии. В поле тяготения Земли нулевым уровнем энергии обладает тело, находящееся на поверхности планеты.
Если тело поднимается, сила тяжести совершает отрицательную работу. Если тело падает, сила тяжести совершает положительную работу.
Пример №3. Шарик массой 100 г скатился с горки длиной 2 м, составляющей с горизонталью угол 30о. Определить работу, совершенную силой тяжести.
Сначала переведем единицы измерения в СИ: 100 г = 0,1 кг. Под действием силы тяжести положение тела относительно Земли изменилось на величину, равную высоте горки. Высоту горки мы можем найти, умножим ее длину на синус угла наклона. Начальная высота равна высоте горки, конечная — нулю. Отсюда:
A = mg(h0 – h) = 0,1∙10(2∙sin30o – 0) =2∙0,5 = 1 (Дж)
Потенциальная энергия протяженного тела
Пример №4. Лежавшую на столе линейку длиной 0,5 м ученик поднял за один конец так, что она оказалась в вертикальном положении. Какую минимальную работу совершил ученик, если масса линейки 40 г?
Переведем единицы измерения в СИ: 40 г = 0,04 кг. Минимальная работа, необходимая для поднятия линейки за один конец, равна:
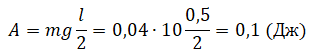
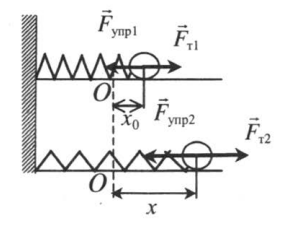
Работа и изменение потенциальной энергии упруго деформированного тела
Вспомним, что работа определяется формулой:
A = Fs cosα
Когда мы сжимаем пружину, шарик перемещается в ту же сторону, в которую направлена сила тяги. Если мы растягиваем ее, шарик перемещается так же в сторону направления силы тяги. Поэтому вектор силы упругости и вектор перемещения сонаправлены, следовательно, угол между ними равен нулю, а его косинус — единице:![]()
Модуль силы тяги равен по модулю силе упругости, поэтому:
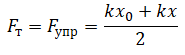
Перемещение определяется формулой:
s = x – x0
Следовательно, работа силы тяги по сжатию или растяжению пружины равна:
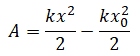
Но известно, что потенциальная энергия упруго деформированного тела равна:
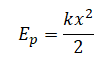
Следовательно, работа силы, под действием которой растягивается или сжимается пружина, равна изменению ее потенциальной энергии:
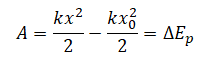

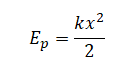
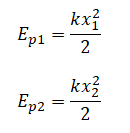
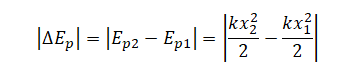
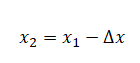
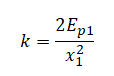
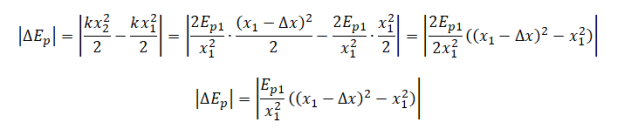
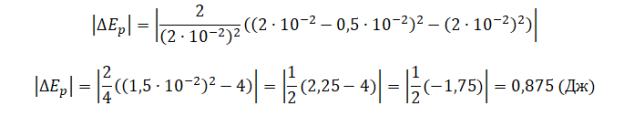
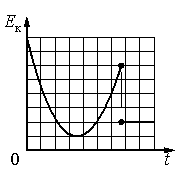 На рисунке представлен схематичный вид графика изменения кинетической энергии тела с течением времени. Какой из представленных вариантов описания движения соответствует данному графику?
На рисунке представлен схематичный вид графика изменения кинетической энергии тела с течением времени. Какой из представленных вариантов описания движения соответствует данному графику?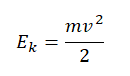
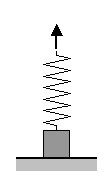 К бруску массой 0,4 кг, лежащему на горизонтальной поверхности стола, прикреплена пружина. Свободный конец пружины тянут медленно в вертикальном направлении (см. рисунок). Определите величину потенциальной энергии, запасённой в пружине к моменту отрыва бруска от поверхности стола, если пружина при этом растягивается на 2 см. Массой пружины пренебречь.
К бруску массой 0,4 кг, лежащему на горизонтальной поверхности стола, прикреплена пружина. Свободный конец пружины тянут медленно в вертикальном направлении (см. рисунок). Определите величину потенциальной энергии, запасённой в пружине к моменту отрыва бруска от поверхности стола, если пружина при этом растягивается на 2 см. Массой пружины пренебречь.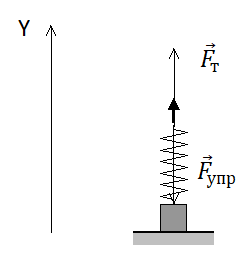
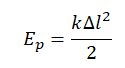
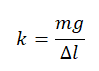
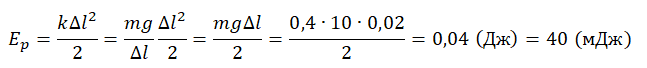
 Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t
Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t
Молодец, хороший разбор задания и пояснение к заданиям.