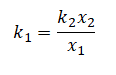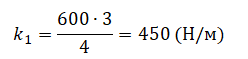Небольшой груз, покоящийся на гладком горизонтальном столе, соединён пружиной со стенкой. Груз немного смещают от положения равновесия вдоль оси пружины и отпускают из состояния покоя, после чего он начинает колебаться, двигаясь вдоль оси пружины, параллельно которой направлена ось Ox. В таблице приведены значения координаты груза х в различные моменты времени t. Выберите все верные утверждения о результатах этого опыта на основании данных, содержащихся в таблице. Абсолютная погрешность измерения координаты равна 0,1 см, времени – 0,05 с.

1) В момент времени 1,50 с ускорение груза максимально.
2) В момент времени 0,50 с кинетическая энергия груза максимальна.
3) Модуль силы, с которой пружина действует на груз, в момент времени 1,00 с меньше, чем в момент времени 0,25 с.
4) Период колебаний груза равен 1 с.
5) Частота колебаний груза равна 0,5 Гц.
Алгоритм решения:
- Проверить истинность утверждения 1. Для этого необходимо установить зависимость ускорения тела, колеблющегося на пружине, от его координаты.
- Проверить истинность утверждения 2. Для этого необходимо установить зависимость кинетической энергии тела, колеблющегося на пружине, от его координаты.
- Проверить истинность утверждения 3. Для этого необходимо записать формулу, отображающую зависимость между силой, действующей на колеблющееся тело, и координатой этого тела. Затем найти модули силы для указанных значений времени и сравнить их.
- Проверить истинность утверждения 4. Для этого необходимо дать определение периоду колебаний, установить период колебаний тела и сравнить его со значением, приведенным в утверждении 4.
- Проверить истинность утверждения 5. Для этого необходимо дать определение частоте колебаний, установить частоту колебаний тела и сравнить его со значением, приведенным в утверждении 5.
- Записать ответ в виде последовательности цифр, не разделенных знаками препинания и пробелами.
Решение:
Проверяем истинность утверждения 1, согласно которому в момент времени 1,50 с ускорение груза максимально. Ускорение груза, колеблющегося на горизонтальной пружине, можно выразить из 2 закона Ньютона (учитываем, что на тело действует сила упругости):
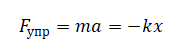
Отсюда ускорение равно:
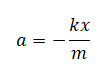
Отношение жесткости пружины к массе груза постоянно, так как эти величины не изменяются. Следовательно, ускорение пропорционально координате колеблющегося тела. И если в момент времени 1,50 с координата тела (отклонение от положения равновесия) максимальна, то ускорение тоже максимально. Однако в соответствии с данными таблицы, в этот момент времени координата тела равна 0,0 см. Следовательно, утверждение 1 неверно.
Проверяем истинность утверждения 2, согласно которому в момент времени 0,50 с кинетическая энергия груза максимальна. Полная механическая энергия тела равна сумме его потенциальной и кинетической энергий:
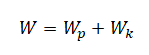
Когда кинетическая энергия груза максимальна, потенциальная энергия равна 0. А потенциальная энергия тела, колеблющегося на пружине, определяется формулой:
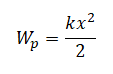
Потенциальная энергия будет равна 0 только в том случае, если в данный момент времени координата тела равна 0 (оно находится в положении равновесия). Следовательно, кинетическая энергия груза в момент времени 0,50 с будет максимальна, если координата тела в это время равна 0. В соответствии с данными таблицы, это действительно так. Следовательно, утверждение 2 верно.
Проверяем истинность утверждения 3, согласно которому модуль силы, с которой пружина действует на груз, в момент времени 1,00 с меньше, чем в момент времени 0,25 с.
Запишем закон Гука:
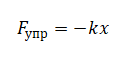
В момент времени 1,00 с координата груза равна –3 см. Так как в данных вычислениях нам нужно лишь сравнить 2 модуля силы, не будем переводить единицы измерения в СИ — для сравнения достаточно, чтобы единицы изменения были одинаковыми. Следовательно, модуль силы упругости в момент времени 1,00 равен:
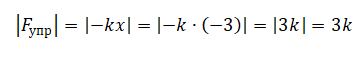
В момент времени 0,25 с координата груза равна 2,1 см. Следовательно, сила упругости равна:
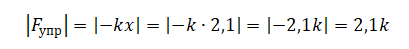
Видно, 3k больше 2,1k. Следовательно, утверждение 3 неверно.
Проверим истинность утверждения 4, согласно которому период колебаний груза равен 1 с. Период — время совершения одного полного колебания. Обозначается буквой T. Единица измерения — секунда (с). Одно полное колебание груз совершает, когда оно возвращается в прежнее положение, пройдя все 4 фазы колебания. Следовательно, если груз начал движение, имея координату 3,0, равную максимальному отклонению от положения равновесия, то периодом будет время, которое ему потребуется для того, чтобы преодолеть положение равновесия, отклониться на максимальное расстояние в обратном положении и вернуться в исходное положение, проходя через точку равновесия.
По таблице видно, что половину колебательного движения груз совершил в момент времени 1,00 с, когда он отклонился на максимальное расстояние в противоположную сторону. Следовательно, столько же времени потребуется грузу, чтобы вернуться в исходное положение. Всего время 1 полного колебания, или период колебаний, составит 2 с. Следовательно, утверждение 4 неверно.
Проверим истинность утверждения 4, согласно которому частота колебаний груза равна 0,5 Гц. Частота — количество колебаний, совершенных в единицу времени. Обозначается как ν («ню»). Единица измерения — 1/секунда, или секунда–1, или герц (1/с, или с–1, или Гц). Частота равна обратной величине периода колебаний:
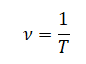
Выше мы выяснили, что период равен 2 с. Следовательно, частота колебаний равна:
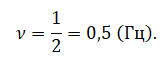
Следовательно, утверждение 5 верно.
Записываем ответ: 25.
Ответ: 25
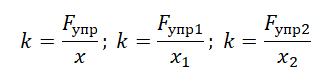
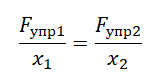
![]()
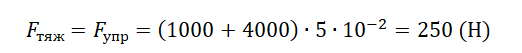
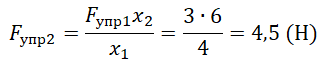

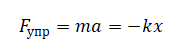
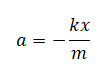
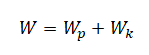
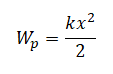
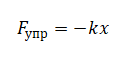
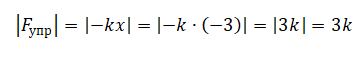
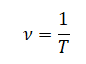
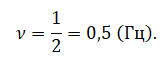
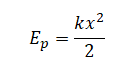
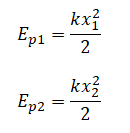
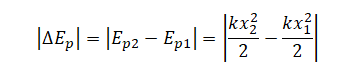
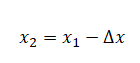
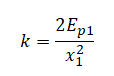
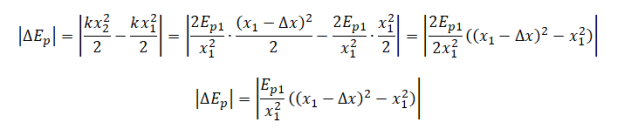
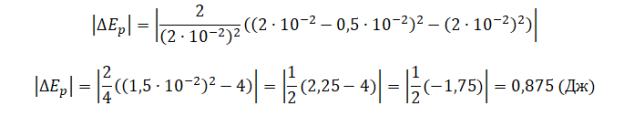
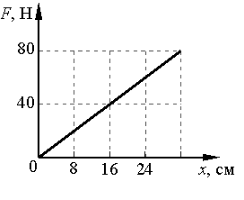 На рисунке представлен график зависимости модуля силы упругости от удлинения пружины. Какова жёсткость пружины?
На рисунке представлен график зависимости модуля силы упругости от удлинения пружины. Какова жёсткость пружины?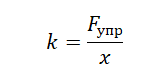
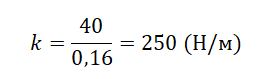
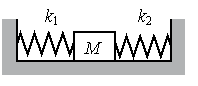 Кубик массой 1 кг покоится на гладком горизонтальном столе, сжатый с боков пружинами (см. рисунок). Первая пружина сжата на 4 см, а вторая сжата на 3 см. Жёсткость второй пружины k2 = 600 Н/м. Чему равна жёсткость первой пружины k1?
Кубик массой 1 кг покоится на гладком горизонтальном столе, сжатый с боков пружинами (см. рисунок). Первая пружина сжата на 4 см, а вторая сжата на 3 см. Жёсткость второй пружины k2 = 600 Н/м. Чему равна жёсткость первой пружины k1?