Вывод формулы
Обратимся к рисунку, который мы использовали для объяснения правила построения изображений в собирающих линзах:
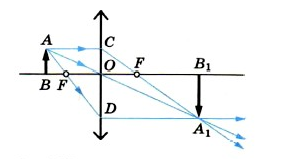
Видно, что треугольники АОВ и А1В1О подобные (по двум углам). Следовательно:
BOOB1=ABA1B1
По двум углам также являются подобными треугольники COF и FA1B1. Отсюда делаем вывод, что:
COA1B1=OFFB1
Линия предмета образует с частью главной оптической оси, перпендикуляром, проведенным из верхней точки к линзе, и частью самой линзы прямоугольник. Следовательно, его противоположные стороны равны:
AB=CO
Следовательно:
ABA1B1=COA1B1
Отсюда следует, что:
BOOB1=OFFB1
BO является расстоянием от предмета до линзы. Обозначим его за d. OB1 является расстоянием от линзы до изображения. Обозначим его за f. OF является фокусным расстоянием линзы. Обозначим его за F. FB1 является разностью расстояния от линзы до изображения и фокусного расстояния линзы. Поэтому это выражение мы можем записать так:
df=Ff−F
Избавимся от знаменателей и получим:
fd−Fd=fF
Или можно записать так:
fF+Fd=fd
Теперь все члены равенства поделим на произведение Ffd. В результате вычислений получим формулу тонкой линзы:
Величины d, ƒ и F могут быть как положительными, так и отрицательными. Отметим (без доказательства), что при применении формулы тонкой линзы знаки нужно ставить перед членами уравнения согласно следующим правилам.
Иногда случается, что перед величинами F, f и d знаки неизвестны. Тогда при вычислениях перед ними ставят знаки «плюс». Но если в результате вычислений фокусного расстояния или расстояния от линзы до изображения либо до источника получается отрицательная величина, то это означает, что фокус, изображение или источник мнимые.
Пример №1. Фокусное расстояние линзы равно 10 см. Найти расстояние от предмета до линзы, если расстояние от нее до изображения составляет 15 см.
Переводить в СИ единицы измерения не будем, поскольку они однородны. Так как все величины выражены в см, то и ответ будет выражен в см.
Применим формулу тонкой линзы:
1d+1f=1F
1d+115=110
Умножим выражение на 150d:
150+10d=15d
5d=150
d=30 (см)
Увеличение линзы
Раньше мы уже упоминали, что изображение, полученное в линзе, может быть увеличенным или уменьшенным. Различие размеров предмета и изображения характеризуется увеличением.
Чтобы найти линейное увеличение изображения предмета в линзе, снова обратимся к первому рисунку этого параграфа. Если высота предмета АВ равна h, а высота изображения А1В1 равна Н, то:
Γ=Hh
Мы уже выяснили, что треугольники АОВ и ОА1В1 подобны. Поэтому:
Hh=|f||d|
Где H — высота изображения предмета, h — высота самого предмета.
Отсюда вытекает, что увеличение линзы равно:
Γ=|f||d|
Пример №2. Предмет имеет высоту h = 2 см. Какое фокусное расстояние F должна иметь линза, расположенная от экрана на расстоянии f = 4 м, чтобы изображение указанного предмета имело высоту H = 1 м?
2 см = 0,02 м
Сначала применим формулы тонкой линзы:
1d+1f=1F
Она необходима, чтобы выразить фокусное расстояние линзы:
F=dfd+f
Расстояние от предмета до линзы неизвестно. Но его можно выразить из формулы увеличения линзы:
Γ=fd=Hh
Отсюда это расстояние равно:
d=fhH
Подставим полученное выражение в формулу фокусного расстояния линзы:
F=fhHffhH+f=f2hH·
Hfh+fH=fhH+h
F=fhH+h=4·0,021+0,02≈0,08 (м)=8 (см)
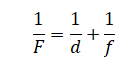
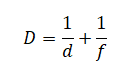
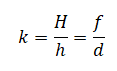
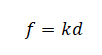
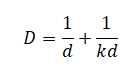
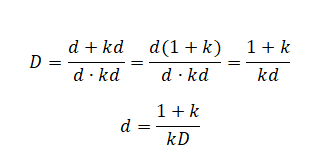
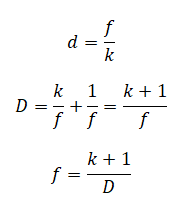
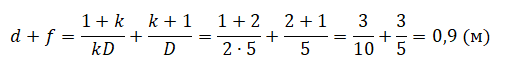
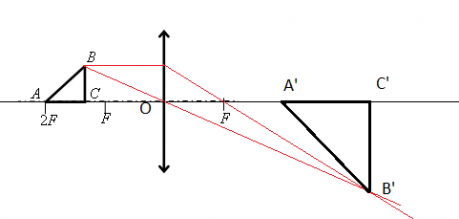
 Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.
Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.