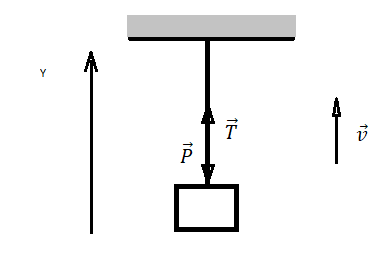
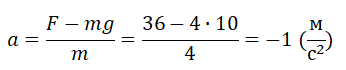Описывая движение тела с помощью законов Ньютона, нужно учитывать все силы, действующие на тело, а также их направления. Определить направления сил вам поможет таблица:
| Сила | Направление |
| Сила тяжести | Вертикально вниз |
| Сила реакции опоры | Перпендикулярно опоре |
| Сила натяжения нити | Вдоль оси подвеса |
| Сила упругости | Противоположно деформации |
| Сила трения | Противоположно скорости или направлению возможного движения |
| Сила сопротивления | |
| Выталкивающая (Архимедова) сила | Вертикально вверх |
Алгоритм решения задач на законы Ньютона
- Запись условий задачи в кратком виде.
- Перевод известных данных в СИ.
- Построение чертежа. На нем отображается само тело, а также направление сил, которые на него действуют. Выбирается система координат, указывается направление ускорения тела.
- Запись второго закона Ньютона в векторном виде.
- Запись второго закона Ньютона в проекциях на оси координат.
- Решение задачи в общем виде (выделение из формулы искомой величины).
- Подстановка в полученную формулу известных данных и вычисление искомой величины.
- Проверка размерности.
Совет! Нужно выбирать такую систему координат, чтобы одна из ее осей совпадала с направлением ускорения движения тела.
Равномерное вертикальное движение (без ускорения)
Сила тяжести и сила реакции опоры |
|||
| Подъем | 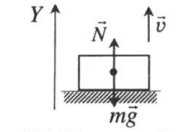 |
Векторная запись II закона Ньютона:
N + mg = ma |
Проекция на ОУ:
N – mg = 0 |
| Спуск | 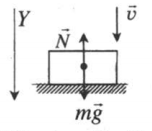 |
Проекция на ОУ:
mg – N = 0 |
|
Сила тяжести и сила натяжения нити |
|||
| Подъем | 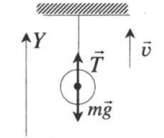 |
Векторная запись II закона Ньютона:
T + mg = ma |
Проекция на ОУ:
T – mg = 0 |
| Спуск | 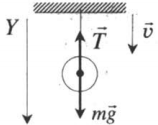 |
Проекция на ОУ:
mg – T = 0 |
|
Сила тяжести и сила сопротивления воздуха |
|||
| Спуск | 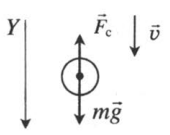 |
Векторная запись II закона Ньютона:
mg + Fc = ma |
Проекция на ОУ:
mg – Fc = 0 |
Сила тяжести, сила сопротивления и Архимедова сила |
|||
| Подъем | 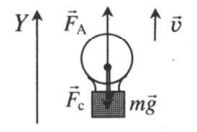 |
Векторная запись II закона Ньютона:
FA + mg + Fc = ma |
Проекция на ОУ:
FA – mg – Fc = 0 |
| Спуск | 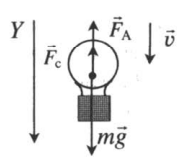 |
Проекция на ОУ:
mg – FA – Fc = 0 |
|
Пример №1. Парашютист массой 80 кг падает при открытом парашюте с установившейся скоростью 5 м/с. Какой будет установившаяся скорость, если на том же парашюте спускается мальчик массой 40 кг. Сила сопротивления воздуха пропорциональна квадрату скорости.
Согласно условию задачи сила сопротивления воздуха пропорциональна квадрату скорости:
Fc = v2
Следовательно, отношение сил сопротивления воздуха парашютиста и мальчика пропорционально отношению квадратов их скоростей:
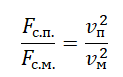
Отсюда:
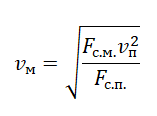
Проекция сил на ось ОУ при равномерном вертикальном движении под действием силы тяжести и силы сопротивления воздуха:
mg – Fc = 0
Силы сопротивления воздуха, действующие на парашютиста и мальчика:
Fc.п. = mпg
Fc.м. = mмg
Следовательно:
Равноускоренное вертикальное движение
Сила тяжести и сила реакции опоры |
|||
| Подъем | 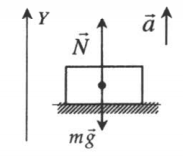 |
Векторная запись II закона Ньютона:
N + mg = ma |
Проекция на ОУ:
N – mg = ma |
| Спуск | 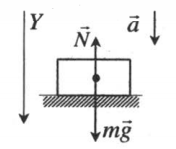 |
Проекция на ОУ:
mg – N = ma |
|
Сила тяжести и сила натяжения нити |
|||
| Подъем | 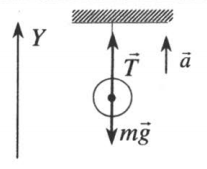 |
Векторная запись II закона Ньютона:
T + mg = ma |
Проекция на ОУ:
T – mg = ma |
| Спуск | 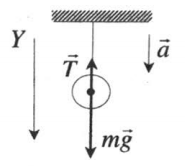 |
Проекция на ОУ:
mg – T = ma |
|
Сила тяжести и сила сопротивления воздуха |
|||
| Подъем | 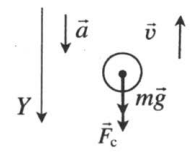 |
Векторная запись II закона Ньютона:
mg + Fc = ma |
Проекция на ОУ:
mg + Fc = ma |
| Спуск | 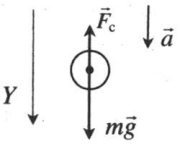 |
Проекция на ОУ:
mg – Fc = ma |
|
Сила тяжести, сила сопротивления и выталкивающая (Архимедова) сила |
|||
| Подъем | 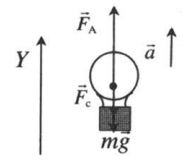 |
Векторная запись II закона Ньютона:
FA + mg + Fc = ma |
Проекция на ОУ:
FA – mg – Fc = ma |
| Спуск | 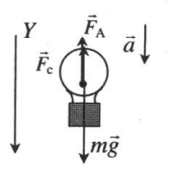 |
Проекция на ОУ:
mg – FA – Fc = ma |
|
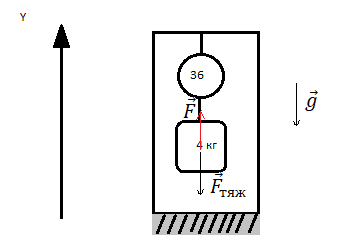
Пример №2. Прочность троса на разрыв составляет 1600 Н. Какой максимальной массы груз можно поднимать этим тросом с ускорением 15 м/с2?
Тело висит на подвесе (тросе) и поднимается ускоренно вверх. Значит, второй закон Ньютона принимает вид:
T – mg = ma
Выразим массу:
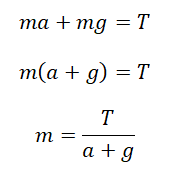
Подставляем известные данные и вычисляем максимальную массу:
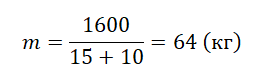
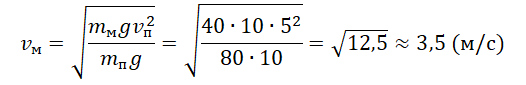
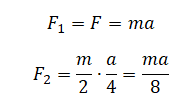
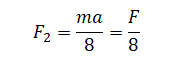
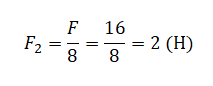
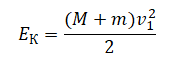
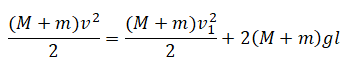
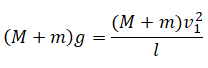
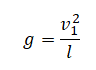
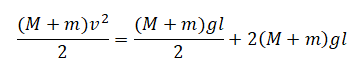
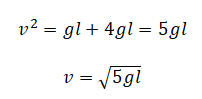
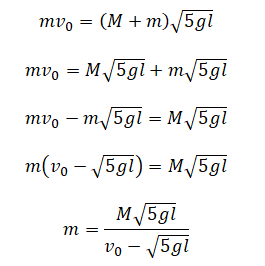
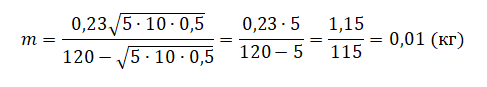
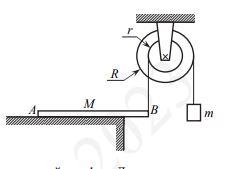 Однородный брусок AB массой M постоянного прямоугольного сечения лежит на гладкой горизонтальной поверхности стола, свешиваясь с него менее чем наполовину (см. рисунок). К правому концу бруска прикреплена лёгкая нерастяжимая нить. Другой конец нити закреплён на меньшем
из двух дисков идеального составного блока. На большем диске этого блока закреплена другая лёгкая
нерастяжимая нить, на которой висит груз массой m = 1 кг. Диски скреплены друг с другом, образуя единое целое. R = 10 см, r = 5 см. Сделайте рисунок с указанием сил, действующих на брусок M, блок и груз m. Найдите минимальное значение M, при котором система тел остаётся неподвижной. Обоснуйте применимость используемых законов к решению задачи.
Однородный брусок AB массой M постоянного прямоугольного сечения лежит на гладкой горизонтальной поверхности стола, свешиваясь с него менее чем наполовину (см. рисунок). К правому концу бруска прикреплена лёгкая нерастяжимая нить. Другой конец нити закреплён на меньшем
из двух дисков идеального составного блока. На большем диске этого блока закреплена другая лёгкая
нерастяжимая нить, на которой висит груз массой m = 1 кг. Диски скреплены друг с другом, образуя единое целое. R = 10 см, r = 5 см. Сделайте рисунок с указанием сил, действующих на брусок M, блок и груз m. Найдите минимальное значение M, при котором система тел остаётся неподвижной. Обоснуйте применимость используемых законов к решению задачи.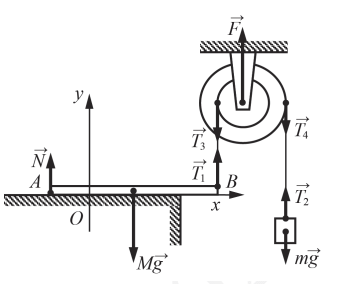
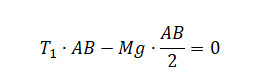
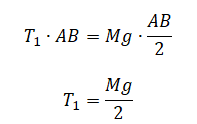
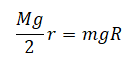
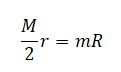
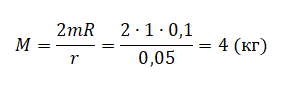
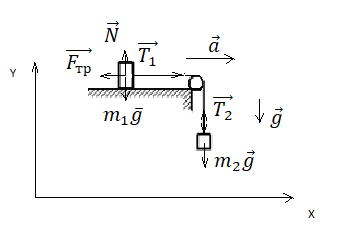
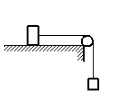 По горизонтальному столу из состояния покоя движется брусок массой 0,9 кг, соединённый с грузом массой 0,3 кг невесомой нерастяжимой нитью, перекинутой через гладкий невесомый блок (см. рисунок). Коэффициент трения бруска о поверхность стола равен 0,2. Натяжение вертикальной части нити равно:
По горизонтальному столу из состояния покоя движется брусок массой 0,9 кг, соединённый с грузом массой 0,3 кг невесомой нерастяжимой нитью, перекинутой через гладкий невесомый блок (см. рисунок). Коэффициент трения бруска о поверхность стола равен 0,2. Натяжение вертикальной части нити равно:
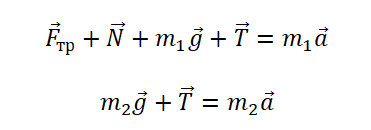
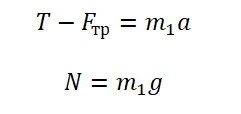
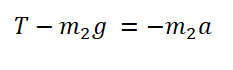
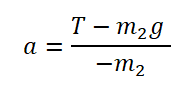
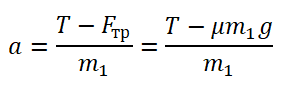
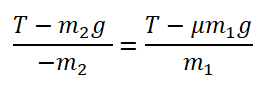

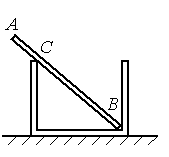 Однородный стержень АВ массой 100 г покоится, упираясь в стык дна и стенки банки концом В и опираясь на край банки в точке С (см. рисунок). Модуль силы, с которой стержень давит на стенку сосуда в точке С, равен 0,5 Н. Чему равен модуль горизонтальной составляющей силы, с которой стержень давит на сосуд в точке В, если модуль вертикальной составляющей этой силы равен 0,6 Н? Трением пренебречь.
Однородный стержень АВ массой 100 г покоится, упираясь в стык дна и стенки банки концом В и опираясь на край банки в точке С (см. рисунок). Модуль силы, с которой стержень давит на стенку сосуда в точке С, равен 0,5 Н. Чему равен модуль горизонтальной составляющей силы, с которой стержень давит на сосуд в точке В, если модуль вертикальной составляющей этой силы равен 0,6 Н? Трением пренебречь.